미분의 이해는 평균변화율부터 시작한다.
미분을 이해하기 위해 첫번째로 이해하려고 하는 것은 변화율이라는 개념이다. 미분 이라는 단어의 정의를 먼저 찾아 읽고 시작하고 싶겠지만 이해는 하나하나 쌓아가는것이고, 섣부른 지식의 섭취는 이해를 방해할 수 도 있기에 천천히 내가 이해한 바를 설명하며 이야기를 풀어나가려고 한다. 이 글을 쓰고 있는 나는 미분을 배워본적이 없는 문과생이었고, 지금도 이해하려 애쓰고 있는 사람이다. 함께 즐겼으면 좋겠다.
*비율: 비율이라는 것은 비교하여 나타내는 관계를 말한다. 전체에 대해 특정 부분이 차지하는 크기라고 할 수 있다.
변화율이라는 것은 말그대로 변화의 비율이다. 무언가가 달라진 변화량의 비율을 나타내는 것이다.
우리가 다룰 변화율의 종류는 두가지가 있는데, 평균변화율과 순간변화율이다. 용어의 의미는 아주 직관적이다. 평균적인 변화율과 순간적인 변화율이라는 말이다.
모눈종이와 같은 *좌표평면을 상상했을때 랜덤하게 선택한 두 점 사이의 함수값의 변화량(y축의 변화량)을 입력값의 변화량(x축의 변화량)으로 나눈 것이다. 좌우로 얼마만큼 이동했는가를 분모로, 위아래로 얼마만큼 이동했는지를 분자로 삼아서(나눠서) 평균을 구한것이다. 그리고 그 평균변화율 이라는 값은 함수f(x)위의 두점사이의 기울기인것이다.
*기울기: 직선이 기울어진 정도, x값 증가량을 분모로, y값 증가량을 분자로 한다. 이 말은 기울어져있는 선이 있을때 그 선의 한쪽끝과 다른쪽 끝이 가로로 얼마만큼 이동했느냐를 분모로 하고 그 선의 한쪽끝과 다른쪽 끝이 세로로는 얼마나 이동했느냐를 분자로 해서 그 비율을 구했을때, 그 선이 얼마나 기울어져있는지가 구해진다는 뜻이다.
*좌표평면: 두개의 수직선이 직각으로 만나 만들어진 평면, 가로선을 x축, 세로선을 y축 이라고한다. 두축이 만나는 점은 0, 원점이다.
*함수: 입력값(정의역,x) -> {함수} -> 출력값(치역,y) / 입력값을 함수에 넣으면 출력값이 되어 나온다.
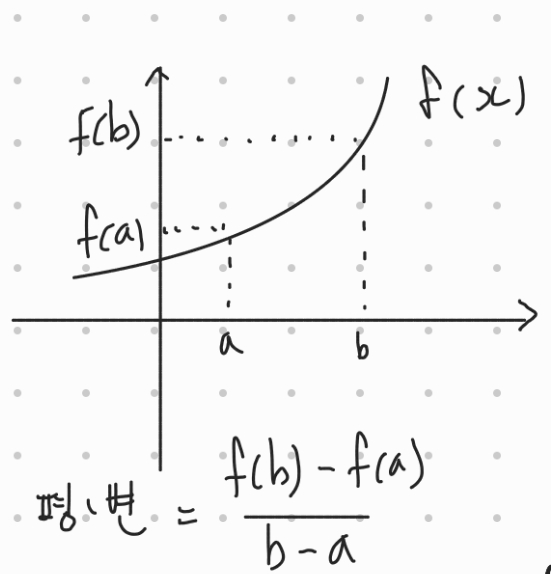
여기서 b-a 라는 것을 x축에서 a에서 b까지 증가한 양 이라고 생각하고 h 라고 표현해보자그러면 b-a=h 이고 a를 우변으로 이동시키면 b=a+h 라고 표현할 수 있다. 그러면 그 b를 위의 식에 대입해 보자.
왜 그래야 하는데? 하는 생각이 들것같은데 일단 먼저 해보고 나서 설명하겠다. 위에 식에 있는 모든 b라는 문자를 a+h로 대체하면
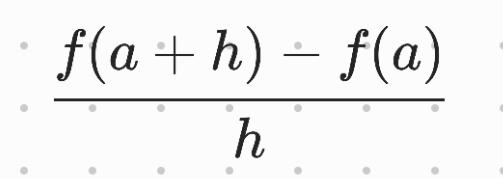
이렇게 된다.
평균 변화율을 표현하는 두가지 방법중, 첫번째 방법은 함수값의 변화에, 두번째 방법은 변수의 변화량 자체에 집중한 표현으로서
우리는 두가지 표현법을 앎으로써 평균변화율 이라는 개념을 더 폭넓게 이해할 수 있고, 다양하게 활용할 수 있다.
순간변화율
순간변화율은 평균변화율과 관계가 있다.
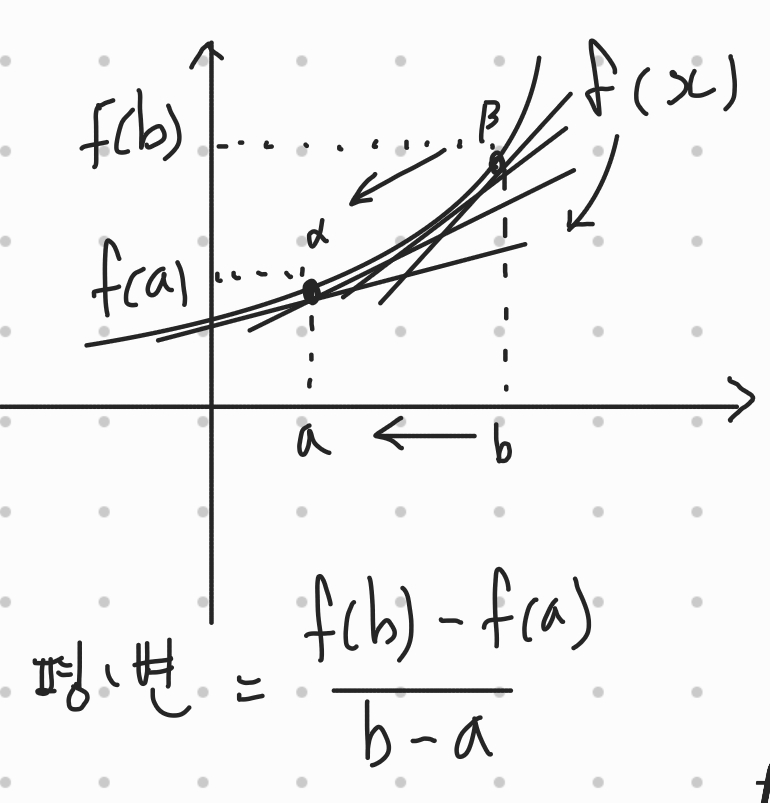
우리가 평균변화율을 구할때 생각했던 a와 b 사이의 거리가 절반으로 줄었다고 생각해보자. 그렇다고 해도 우리는 여전히 평균변화율(기울기)을 구할 수 있다. 둘사이의 거리가 또 한번 절반으로 줄었다고 해도 우리는 두점사이의 기울기를 구할수 있을것이다.
이 과정을 계속 반복하면 (반에 반에 반에 반에…) 우리는 아주 찰나의, (x축을 시간이라고 생각해보자)순간적으로 두점사이의 거리가 거의 차이가 없을정도의 (한 점으로 느껴질정도로) 아주 작은 순간의 기울기 또한 구할 수 있을것이다. 그것을 순간변화율이라고 한다.
그리고 그 순간변화율을 구하는 방법은 평균변화율을 두 점사이의 거리 (=a에서b까지 증가한 양 = h)인 h가 0이될때, 0으로 한없이(계속해서) 가까이갈때의 평균변화율을 구하면 된다. 어떤 함수의 입력값이-우리의 경우에는 평균변화율이라는 함수다- 특정한 값으로 가까이 갈때 그 함수값은 어디로 가까이 가는지를 구하는것이 극한이라는 것의 개념이고, 우리는 평균변화율의 극한값을 구하여 순간변화율을 구할 수 있다.
드리는 말씀
미분을 이해하는 것에는 기본적으로 함수와 좌표평면에대한 이해가 필요합니다. 미분에 대한 본격적인 공부를 하기 전에 극한에 대한 개념또한 공부를 해보면 재미가 있습니다. 줄글수학이라는 컨텐츠는 가볍게 읽는 워밍업으로 생각해주시면 감사하겠습니다. 최대한 숙고하는 일없이 부드럽게 읽히도록 서술하겠습니다.